Difference between revisions of "Import From ORCID"
| Line 1: | Line 1: | ||
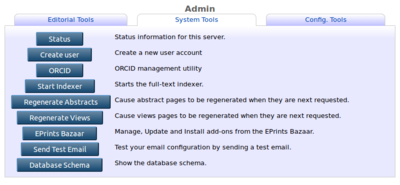
| − | [[File:import_from_orcid_admin.png|400px|thumb|left|After installing, an ORCID button appears on the Admin screen]] | + | [[File:import_from_orcid_admin.png|400px|thumb|left|1. After installing, an ORCID button appears on the Admin screen]] |
| − | [[File:import_from_orcid_enter_orcid.png|400px|thumb|left|]] | + | [[File:import_from_orcid_enter_orcid.png|400px|thumb|left|2. Enter an ORCID to search for published works]] |
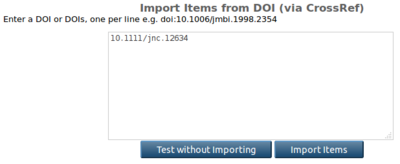
| − | [[File:import_from_orcid_search_results.png|400px|thumb|left|]] | + | [[File:import_from_orcid_search_results.png|400px|thumb|left|3. Search results showing import options (import from DOI or import from PubMed ID)]] |
| − | [[File:import_from_orcid_import.png|400px|thumb|left|]] | + | [[File:import_from_orcid_import.png|400px|thumb|left|4. Clicking Import takes you to the standard Import screen]] |
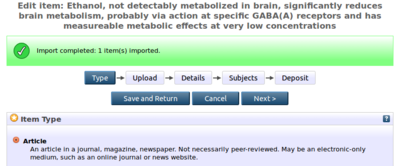
| − | [[File:import_from_orcid_edit_item.png|400px|thumb|left|]] | + | [[File:import_from_orcid_edit_item.png|400px|thumb|left|5. After importing the item]] |